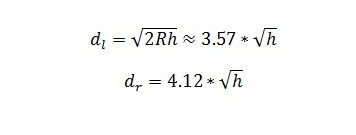Calculateur de Facteur de Bruit vers Figure de Bruit

Le calculateur de facteur de bruit permet de convertir le facteur de bruit d’un composant ou d’un système RF en figure de bruit (Noise Figure, NF) en dB.
Cet outil est essentiel pour évaluer la performance des amplificateurs, récepteurs et autres circuits RF.

Formule utilisée

NF = 10 × log₁₀(F)

où :
F = facteur de bruit (linéaire, ≥ 1)
NF = figure de bruit en décibels (dB)

Explication

La formule convertit le facteur de bruit linéaire F en une valeur logarithmique NF exprimée en dB.
Une figure de bruit plus faible indique un composant ou système plus performant, avec moins de dégradation du rapport signal/bruit.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes électroniques pour :

  • Évaluer la performance des amplificateurs et récepteurs.
  • Comparer différents composants RF selon leur bruit.
  • Optimiser le design des systèmes pour minimiser le bruit global.

Exemple de calcul

Pour un composant avec un facteur de bruit :
F = 2 (linéaire) :
NF = 10 × log₁₀(2) ≈ 3.01 dB

Conseils de calcul

  • Assurez-vous que le facteur de bruit F est supérieur ou égal à 1.
  • Vérifiez les valeurs fournies par le fabricant ou les mesures expérimentales.
  • Utilisez cette conversion pour planifier la chaîne RF et garantir un bon rapport signal/bruit.

Pourquoi ce calcul est utile

La conversion du facteur de bruit en figure de bruit permet de mieux comparer les composants RF et d’optimiser les performances du système,
en particulier dans les applications sensibles au bruit comme les récepteurs et les amplificateurs à faible bruit.

Calculateur de Facteur de Bruit à partir du Bruit de Figure

Le calculateur de facteur de bruit permet de convertir le bruit de figure (Noise Figure, NF) d’un dispositif RF en facteur de bruit linéaire (Noise Factor, F).
Cet outil est essentiel pour évaluer la performance des amplificateurs et autres composants RF.

dB

Formule utilisée

F = 10^(NF / 10)

où :
NF = bruit de figure en dB
F = facteur de bruit linéaire

Explication

La formule convertit le bruit de figure en décibels en facteur de bruit linéaire.
Un facteur de bruit plus faible indique un composant plus performant, contribuant moins au bruit total du système.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes électroniques pour :

  • Évaluer la contribution au bruit des amplificateurs et dispositifs RF.
  • Comparer différents composants pour choisir les plus performants.
  • Optimiser la conception globale des chaînes RF et améliorer le rapport signal/bruit.

Exemple de calcul

Pour un composant avec :
NF = 3 dB :
F = 10^(3/10) ≈ 2

Conseils de calcul

  • Vérifiez que la valeur de NF est correctement mesurée ou fournie par le fabricant.
  • Utilisez ce calcul pour évaluer l’impact du bruit dans les systèmes RF complexes.

Pourquoi ce calcul est utile

Connaître le facteur de bruit permet de prévoir la performance du système, d’améliorer le rapport signal/bruit et de sélectionner les composants RF les plus adaptés pour une conception optimale.

Calculateur de VSWR vers Return Loss

Le calculateur VSWR vers Return Loss permet de convertir le rapport d’onde stationnaire en tension (VSWR) en perte de retour (Return Loss, RL).
Cet outil est utile pour les ingénieurs RF afin de vérifier l’adaptation d’impédance et la qualité des lignes de transmission.

Formule utilisée

RL (dB) = -20 × log10((VSWR – 1) / (VSWR + 1))

où :
VSWR = rapport d’onde stationnaire en tension (≥1)
RL = perte de retour en décibels (dB)

Explication

Cette formule convertit le VSWR en Return Loss pour quantifier combien de signal est réfléchi dans une ligne de transmission.
Un RL plus élevé indique une meilleure adaptation d’impédance et moins de pertes par réflexion.

Utilisation

Cet outil est utilisé par les ingénieurs RF et techniciens pour :

  • Évaluer l’efficacité des lignes de transmission et des antennes.
  • Vérifier l’adaptation d’impédance dans les systèmes RF.
  • Identifier les points de réflexion et optimiser les performances du signal.

Exemple de calcul

Pour une ligne avec VSWR = 1.5 :
RL = -20 × log10((1.5 – 1) / (1.5 + 1)) ≈ 9.54 dB

Conseils de calcul

  • Assurez-vous que le VSWR est supérieur ou égal à 1.
  • Utilisez ce calcul pour comparer différentes lignes ou configurations d’antenne.
  • Une RL supérieure indique une meilleure performance et moins de réflexion.

Pourquoi ce calcul est utile

Connaître le Return Loss à partir du VSWR permet de contrôler l’efficacité des systèmes RF,
d’optimiser les lignes de transmission et de réduire les pertes de signal causées par des désadaptations d’impédance.

Calculateur de Réactance et Admittance Inductive

Le calculateur de réactance et admittance inductive permet de déterminer la réactance inductive (XL) et l’admittance inductive (BL) d’une inductance à une fréquence donnée.
Cet outil est utile pour les ingénieurs RF et les concepteurs de circuits électroniques.

Enter F and L to calculate for XL and BL

Formule utilisée

XL = 2π × f × L
BL = 1000 / XL

où :
f = fréquence du signal (Hz, kHz, MHz, GHz)
L = inductance (H, mH, µH, nH)
XL = réactance inductive en ohms (Ω)
BL = admittance inductive en milli-mhos

Explication

La réactance inductive XL représente la résistance au passage du courant alternatif due à l’inductance.
L’admittance BL est l’inverse de cette réactance, exprimée en milli-mhos, et indique la facilité avec laquelle le courant passe à travers l’inducteur.

Utilisation

Cet outil est utilisé par les ingénieurs et techniciens pour :

  • Calculer la réactance et l’admittance d’inductances dans des circuits AC.
  • Analyser les filtres, oscillateurs et circuits résonants.
  • Aider à la conception et à l’optimisation de composants RF et électroniques.

Exemple de calcul

Pour une inductance de 100 nH à une fréquence de 1 GHz :
XL = 2π × 1×10⁹ × 100×10⁻⁹ ≈ 628,32 Ω
BL = 1000 / 628,32 ≈ 1,591 m-mhos

Conseils de calcul

  • Assurez-vous d’utiliser des unités cohérentes pour la fréquence et l’inductance.
  • Vérifiez que les valeurs de fréquence et d’inductance sont positives et réalistes.
  • Comparez différents composants pour optimiser les performances des circuits AC.

Pourquoi ce calcul est utile

Connaître la réactance et l’admittance inductive permet de concevoir et d’analyser correctement les circuits AC, d’optimiser les filtres et oscillateurs,
et de garantir la performance des systèmes RF et électroniques.

Calculateur de Fréquence vers PPM (Parts Par Million)

Le calculateur Hz vers PPM permet de convertir la variation de fréquence d’un oscillateur en parties par million (ppm).
Cet outil est utile pour les ingénieurs RF et les techniciens qui doivent évaluer la précision et la stabilité des oscillateurs.

Formule utilisée

PPM = (Δf / f₀) × 10⁶

où :
f₀ = fréquence centrale ou fréquence d’oscillation (Hz, kHz, MHz, GHz)
Δf = variation de fréquence (Hz, kHz, MHz, GHz)
PPM = parties par million

Explication

Cette formule montre que le décalage en ppm est proportionnel à la variation de fréquence par rapport à la fréquence centrale de l’oscillateur.
Une variation plus faible ou une fréquence plus élevée réduit la valeur en ppm, indiquant une meilleure stabilité.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de circuits pour :

  • Mesurer la précision des oscillateurs et des horloges.
  • Comparer la stabilité de différents composants RF.
  • Aider à concevoir des systèmes de communication fiables.

Exemple de calcul

Pour un oscillateur avec :
f₀ = 10 MHz, Δf = 50 Hz :
PPM = (50 / 10 000 000) × 10⁶ ≈ 5 ppm

Conseils de calcul

  • Assurez-vous que la fréquence centrale et la variation sont dans des unités cohérentes.
  • Vérifiez que la fréquence centrale est supérieure à zéro pour éviter des résultats incorrects.
  • Utilisez ce calcul pour évaluer et comparer différents oscillateurs.

Pourquoi ce calcul est utile

Connaître le décalage en ppm permet de mesurer la précision des oscillateurs et d’optimiser la performance des systèmes RF et électroniques sensibles à la stabilité de fréquence.

Calculateur de Conversion Longueur d’Onde vers Fréquence

Le calculateur de longueur d’onde vers fréquence permet de convertir la longueur d’onde d’un signal électromagnétique en sa fréquence correspondante.
Cet outil est essentiel pour les ingénieurs RF et les techniciens travaillant sur les systèmes de communication et de transmission.

Formule utilisée

f = c / λ

où :
f = fréquence (Hz, MHz)
λ = longueur d’onde (m, cm, mm, µm, nm)
c = vitesse de la lumière (~3 × 10⁸ m/s)

Explication

La fréquence d’un signal électromagnétique est inversement proportionnelle à sa longueur d’onde.
Plus la longueur d’onde est courte, plus la fréquence est élevée.
Cette relation est fondamentale pour le dimensionnement des antennes et des systèmes RF.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes électroniques pour :

  • Déterminer la fréquence correspondant à une longueur d’onde donnée.
  • Aider au dimensionnement et à la conception des antennes et circuits RF.
  • Analyser les performances des systèmes de transmission et de communication.

Exemple de calcul

Pour une longueur d’onde de 0,15 m :
f = 3 × 10⁸ / 0,15 ≈ 2 000 MHz

Conseils de calcul

  • Vérifiez que la longueur d’onde est exprimée dans l’unité correcte avant de calculer.
  • Pour des conversions précises, utilisez des valeurs exactes de la vitesse de la lumière selon le milieu (air, vide, autre).
  • Testez différentes unités de longueur d’onde pour valider les conversions.

Pourquoi ce calcul est utile

Connaître la fréquence à partir de la longueur d’onde est crucial pour la conception et l’analyse des systèmes RF,
la planification des bandes de communication et l’optimisation des performances des antennes.

Calculateur de Fréquence vers Longueur d’Onde

Le calculateur de fréquence vers longueur d’onde permet de convertir une fréquence donnée en sa longueur d’onde correspondante dans l’air ou le vide.
Cet outil est utile pour les ingénieurs RF et les concepteurs de systèmes de communication et d’antenne.

Formule utilisée

λ = c / f

où :
λ = longueur d’onde (mètres)
c = vitesse de la lumière (~299 792 458 m/s)
f = fréquence (Hz, kHz, MHz, GHz)

Explication

Cette formule montre que la longueur d’onde est inversement proportionnelle à la fréquence.
Une fréquence plus élevée correspond à une longueur d’onde plus courte et vice versa.
Cette relation est fondamentale pour la conception des antennes et la propagation des ondes électromagnétiques.

Utilisation

Ce calculateur est utilisé par les ingénieurs RF et les techniciens pour :

  • Déterminer la longueur d’onde pour la conception d’antennes et de lignes de transmission.
  • Analyser la propagation des signaux dans différents systèmes de communication.
  • Optimiser la performance des systèmes RF en fonction de la fréquence utilisée.

Exemple de calcul

Pour une fréquence de :
f = 100 MHz :
λ = 299 792 458 / 100 000 000 ≈ 2,998 mètres

Conseils de calcul

  • Vérifiez que la fréquence est saisie dans la bonne unité et convertissez si nécessaire.
  • Utilisez ce calcul pour choisir la taille correcte des antennes et optimiser la réception ou l’émission.
  • Pour des fréquences très élevées, vérifiez que les arrondis ne réduisent pas la précision.

Pourquoi ce calcul est utile

Connaître la longueur d’onde permet de dimensionner correctement les antennes, d’évaluer la propagation des ondes et d’optimiser la performance des systèmes RF et de communication.

Calculateur de Conversion Watt vers dBm

Le calculateur Watt vers dBm permet de convertir la puissance exprimée en watts en décibels milliwatts (dBm).
Cet outil est essentiel pour les ingénieurs RF et les techniciens qui travaillent sur les systèmes de transmission et de communication.

W

Formule utilisée

dBm = 10 × log₁₀(P × 1000)

où :
P = puissance en watts (W)
dBm = puissance exprimée en décibels milliwatts

Explication

La formule convertit la puissance linéaire en watts en une échelle logarithmique en dBm.
Multiplier par 1000 permet de passer de watts à milliwatts, et le logarithme base 10 exprime la puissance en décibels.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes pour :

  • Comparer la puissance des signaux dans différentes unités.
  • Dimensionner correctement les amplificateurs et les émetteurs.
  • Analyser et optimiser les systèmes de transmission RF.

Exemple de calcul

Pour une puissance de 0,05 W :
dBm = 10 × log₁₀(0,05 × 1000) ≈ 16,9897 dBm

Conseils de calcul

  • Assurez-vous que la valeur en watts est positive et réaliste.
  • Vérifiez l’unité de puissance avant de convertir pour éviter des erreurs.
  • Utilisez cette conversion pour toutes les analyses RF nécessitant des comparaisons logarithmiques.

Pourquoi ce calcul est utile

La conversion en dBm permet d’évaluer facilement les niveaux de puissance sur une échelle logarithmique,
de comparer différents équipements RF et de planifier correctement les systèmes de transmission.

Calculateur de Conversion dBm en Watt

Le calculateur dBm vers Watt permet de convertir une valeur de puissance exprimée en dBm en Watts.
Cet outil est utile pour les ingénieurs RF et les techniciens souhaitant interpréter et comparer facilement les puissances dans différents systèmes électroniques.

dBm

Formule utilisée

P(W) = 10^(P(dBm)/10) / 1000

où :
P(dBm) = puissance en dBm
P(W) = puissance en Watts

Explication

Cette formule convertit la puissance logarithmique (dBm) en puissance linéaire (Watts).
La division par 1000 convertit la valeur de milliwatts en Watts.
Cette conversion est essentielle pour comparer les puissances avec d’autres unités ou pour le dimensionnement des circuits.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes pour :

  • Convertir rapidement les mesures de puissance dBm en Watts.
  • Évaluer la puissance réelle transmise ou reçue dans les systèmes RF.
  • Aider à la conception et au calcul des composants électroniques.

Exemple de calcul

Pour une puissance de 30 dBm :
P(W) = 10^(30/10) / 1000 = 1 Watt

Conseils de calcul

  • Assurez-vous que la valeur en dBm est correcte et cohérente avec votre système.
  • Vérifiez si vous avez besoin de la puissance en milliwatts ou en Watts pour vos calculs.
  • Utilisez cette conversion pour dimensionner correctement vos amplificateurs et antennes.

Pourquoi ce calcul est utile

La conversion dBm en Watts permet d’interpréter facilement les puissances dans les systèmes RF,
d’assurer une conception correcte des circuits et de comparer les puissances entre différents équipements.

Calculateur de Ligne de Vue (Line of Sight)

Le calculateur de ligne de vue permet de déterminer la distance à laquelle une antenne peut « voir » une autre antenne sans obstacles.
Cet outil est utile pour la planification des réseaux radio, la couverture de communication et l’optimisation des systèmes RF.

Formule utilisée

dₗ = 3,57 × √h
dᵣ = 4,12 × √h

où :
h = hauteur de l’antenne (mètres ou pieds)
dₗ = distance de ligne de vue (km)
dᵣ = horizon radio ou portée du service (km)

Explication

La formule dₗ calcule la distance directe de ligne de vue à partir de la hauteur de l’antenne, tandis que dᵣ prend en compte l’effet de la courbure de la Terre et fournit la portée pratique de service.
Plus l’antenne est haute, plus la distance de couverture augmente.

Utilisation

Cet outil est utilisé par les ingénieurs RF et planificateurs réseau pour :

  • Évaluer la distance maximale de communication entre antennes.
  • Planifier la couverture des systèmes radio et micro-ondes.
  • Optimiser le positionnement des antennes pour une portée maximale.

Exemple de calcul

Pour une antenne de hauteur :
h = 25 m :
dₗ = 3,57 × √25 ≈ 17,85 km
dᵣ = 4,12 × √25 ≈ 20,60 km

Conseils de calcul

  • Utilisez des unités cohérentes (mètres ou pieds) pour la hauteur de l’antenne.
  • Vérifiez que l’environnement autour des antennes est dégagé pour une ligne de vue optimale.
  • Testez différents emplacements et hauteurs pour comparer la portée.

Pourquoi ce calcul est utile

Connaître la ligne de vue et l’horizon radio permet de planifier efficacement les réseaux RF,
d’assurer une couverture maximale et d’éviter les zones mortes dans les systèmes de communication.

Calculateur de Bruit de Phase vers Gigue

Le calculateur de bruit de phase permet de convertir le bruit de phase intégré d’un oscillateur en gigue RMS.
Cet outil est utile pour analyser la stabilité des signaux dans les systèmes RF et électroniques.

dBc

Formule utilisée

Jrad = √(2 × 10^(A/10))
Jµs = Jrad / (2π × f₀) × 10⁶

où :
A = bruit de phase intégré en dBc
f₀ = fréquence de l’oscillateur (Hz, kHz, MHz, GHz)
Jrad = gigue RMS en radians
Jµs = gigue RMS en microsecondes

Explication

La première formule calcule la gigue RMS en radians à partir du bruit de phase intégré.
La seconde convertit cette gigue en microsecondes en fonction de la fréquence de l’oscillateur.
Une gigue plus faible signifie un signal plus stable et précis.

Utilisation

Cet outil est utilisé par les ingénieurs RF et les concepteurs de systèmes électroniques pour :

  • Évaluer la stabilité temporelle des oscillateurs.
  • Prévoir les performances des circuits RF sensibles à la gigue.
  • Optimiser la conception des systèmes de communication et de synchronisation.

Exemple de calcul

Pour un oscillateur avec :
f₀ = 10 kHz, A = -80 dBc :
Jrad = √(2 × 10^(-80/10)) ≈ 1.414 × 10⁻⁴ rad
Jµs = (1.414 × 10⁻⁴) / (2π × 10 000) × 10⁶ ≈ 2.25 µs

Conseils de calcul

  • Vérifiez que les unités de fréquence et de bruit de phase sont cohérentes.
  • Assurez-vous que le bruit de phase intégré est mesuré sur la bande de fréquence d’intérêt.
  • Utilisez ce calcul pour comparer différents oscillateurs ou configurations de circuits.

Pourquoi ce calcul est utile

Connaître la gigue RMS permet de planifier et d’optimiser la conception des systèmes RF et électroniques,
d’assurer la précision des signaux et d’améliorer la fiabilité des communications.

Les Types de Diversité en Télécommunications

Les Types de Diversité en Télécommunications

Les signaux transmis dans un environnement de télécommunications sont souvent affectés par des phénomènes comme la perte de signal, l’évanouissement ou les interférences. Pour garantir une meilleure qualité de transmission, différentes techniques de diversité sont employées. Aujourd’hui, on va voir les principaux types de diversité utilisés en télécommunications, leurs principes, leurs avantages, ainsi que leur mise en œuvre concrète.

Qu’est-ce que la diversité en télécommunications ?

La diversité est une méthode consistant à utiliser plusieurs chemins ou plusieurs versions du même signal afin de réduire les effets négatifs des perturbations sur la qualité de la communication. Elle permet de compenser les pertes ou dégradations liées au canal de transmission en sélectionnant ou combinant les signaux reçus de manière optimale.

Types principaux de diversité

Les types de diversité se distinguent principalement par la dimension sur laquelle ils reposent : l’espace, le temps, la fréquence, ou même la polarisation. Chacun répond à des problématiques spécifiques du canal radio et peut être combiné avec d’autres pour améliorer la robustesse globale.

    1. Diversité spatiale (Espace)

La diversité spatiale repose sur l’utilisation de plusieurs antennes situées à des positions différentes. L’objectif est de capter plusieurs versions du signal qui ont subi des trajets de propagation distincts, donc des évanouissements différents.

      • Principe : Les signaux reçus par différentes antennes ont une probabilité moindre d’être simultanément affectés par un affaiblissement sévère.
      • Mise en œuvre : Plusieurs antennes sont disposées à une distance suffisante (généralement plusieurs longueurs d’onde) pour assurer une indépendance des signaux reçus.
      • Avantages : Amélioration significative de la qualité de réception, réduction des erreurs de transmission.
      • Applications : MIMO (Multiple Input Multiple Output), antennes diversity dans les stations de base et terminaux mobiles.
    2. Diversité temporelle (Temps)

Cette technique consiste à transmettre le même signal à différents instants, en séparant les copies par un intervalle suffisant pour que les perturbations affectant le canal soient indépendantes d’un envoi à l’autre.

      • Principe : Profiter de la variabilité temporelle du canal pour éviter que tous les signaux soient dégradés simultanément.
      • Mise en œuvre : Utilisation de répétitions temporelles ou de codage avec interleaving temporel.
      • Avantages : Permet de corriger les erreurs dues à des fades rapides.
      • Limite : Augmente la latence, car le signal est répété ou retardé.
    2. Diversité fréquentielle (Fréquence)

Elle exploite la transmission simultanée du même signal sur différentes fréquences. Les perturbations étant souvent localisées en fréquence, cette diversité assure qu’au moins une des fréquences porte le signal correctement.

      • Principe : Envoyer plusieurs copies du signal sur des canaux fréquentiels séparés de façon à ce qu’ils subissent des fades indépendants.
      • Mise en œuvre : Utilisation de techniques comme le Frequency Hopping ou le OFDM avec codage sur sous-porteuses distinctes.
      • Avantages : Résistance aux interférences et aux fades sélectifs en fréquence.
    2. Diversité de polarisation

Elle consiste à transmettre ou recevoir le signal avec des antennes de polarisation différentes (verticale, horizontale, circulaire). Les signaux polarisés différemment subissent des atténuations distinctes.

    • Principe : Exploiter des plans de polarisation différents pour obtenir plusieurs versions indépendantes du signal.
    • Mise en œuvre : Antennes à double polarisation ou polarisation croisée.
    • Applications : Utilisée dans certains systèmes radar et dans la téléphonie mobile pour améliorer la qualité.

Comparaison et complémentarité des types de diversité

Les Types de Diversité en Télécommunications

Techniques de combinaison des signaux diversifiés

Après réception de plusieurs copies du signal, il est nécessaire de les combiner pour tirer parti de la diversité. Différentes méthodes existent :

  • Sélection de la meilleure antenne (Selection Combining) : on choisit la copie du signal avec la meilleure qualité.
  • Combinaison maximale de rapport signal sur bruit (Maximal Ratio Combining) : on pondère et additionne les signaux pour maximiser la qualité globale.
  • Combinaison par égalisation (Equal Gain Combining) : on somme les signaux en leur donnant le même poids.

Le choix de la méthode dépend des contraintes de complexité, performance et coût du système.

Exemple simple d’application : la diversité spatiale dans un téléphone mobile

Un téléphone équipé de deux antennes placées à des positions différentes permet de capter deux versions du signal provenant de la station de base. En cas de perturbation sur l’une des antennes, la seconde peut fournir un signal plus clair. Le téléphone combine ces deux signaux, améliorant la qualité de la communication et réduisant les coupures.

Ce principe est largement utilisé dans les technologies LTE et 5G via les systèmes MIMO, qui augmentent non seulement la robustesse mais aussi le débit.

Pour aller plus loin, il serait intéressant d’explorer comment la diversité est intégrée dans les systèmes MIMO avancés et les schémas de codage associés.